What is ECDSA in Bitcoin?

ECDSA (short for Elliptic Curve Digital Signature Algorithm) is a digital-signature scheme built on elliptic-curve cryptography (ECC).

The ECDSA algorithm uses an elliptic curve and a finite field to create a signature on data such that third parties can verify its authenticity, while only the signer can produce it. In Bitcoin, the signed data are transactions that transfer ownership.

The cryptography behind digital-signature schemes in cryptocurrencies enables transaction verification between two parties in a decentralised network.

ECC offers a major advantage over RSA: it achieves the same security with much smaller key sizes. Although RSA remains more common on today’s internet, ECC is a more efficient alternative—which is why cryptocurrencies use it.

Bitcoin’s technology rethinks ownership. Traditionally, to own something—a house, cash and so on—means either holding it (physically or legally) yourself or entrusting it to a custodian such as a bank.

Bitcoin works differently. Coins are not stored centrally or locally, and no single entity acts as custodian.

Bitcoins exist as records on the the blockchain, copies of which are distributed across a network of connected computers. To “own” bitcoin is to be able to transfer control of it to another user by creating a transfer record on the blockchain. What enables that? Access to an ECDSA key pair: a public key and a private key.

ECDSA has distinct procedures for signing and verification. Each is an algorithm consisting of several arithmetic operations. The signing algorithm uses the private key; the verification algorithm uses the public key.

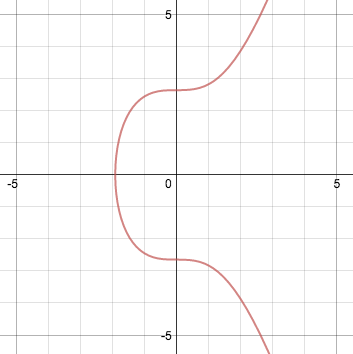
Algebraically, an elliptic curve is given by an equation of the form y2 = x3 + ax + b. For a = 0 and b = 7 (the version used by Bitcoin), it looks like this:

Elliptic curves have useful properties. For example, any non-vertical line that intersects the curve at two points will always intersect a third point on the curve. Another property: a non-vertical tangent line touching the curve at one point will intersect a second point on the curve. These properties define two operations: point addition and point doubling.

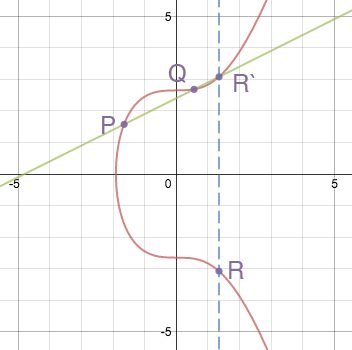
For point addition, P + Q = R, draw a straight line through points P and Q; it meets the curve at a third point R.

Then find the point on the curve symmetric to that third point R across the x-axis. That point R is the sum of P and Q. Example:

Similarly, for point doubling, draw the tangent line to the elliptic curve at point P; it intersects at another point R.

The point R symmetric to R’ across the x-axis is the double of P. Example:

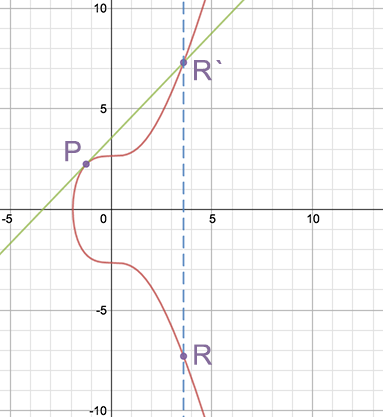
Together, these operations are used for scalar multiplication, R = a P, defined as adding point P to itself a times. For example:

R = 7P
R = P + (P + (P + (P + (P + (P + P)))))

Scalar multiplication is typically simplified by combining point doublings and additions.

For example:

R = 7P
R = P + 6P
R = P + 2 (3P)
R = P + 2 (P + 2P)

Here, 7P is broken into two point doublings and two point additions.

In ECDSA, a finite field can be thought of as a fixed range of positive numbers into which every calculation must fall. Any number outside the range is wrapped back into it. If a result exceeds the range, it wraps from the end to the start and computation continues.

The simplest way to view this is as the remainder operation, or modulus (mod). For instance, 9/7 gives 1 with remainder 2: 9 mod 7 = 2. Here, the finite field is 0 to 6, and any operation modulo 7—on any input—yields a result in that range.

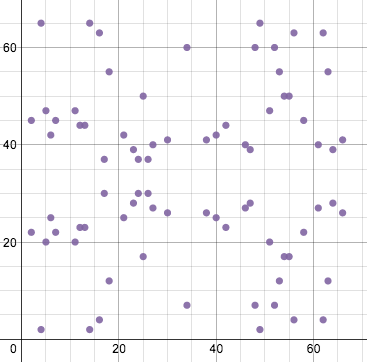
ECDSA uses elliptic curves over a finite field, which changes their appearance but not the underlying formulas or properties. The same equation shown above, over the finite field modulo 67, looks like this:

It becomes a set of points where all x and y values are integers between 0 and 66. The curve still retains horizontal symmetry.

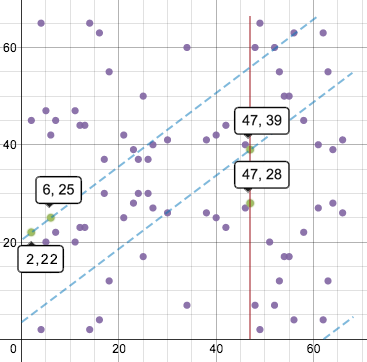
Point addition and doubling look a bit different. Lines drawn on this graph wrap around the field while preserving their slope. Thus, adding points (2, 22) and (6, 25) looks like this:

The wrapping line passing through the two points eventually hits a third point, (47, 39); its reflection across the x-axis is (47, 28). That point is the result of the operation.

A protocol such as Bitcoin fixes a set of parameters for the elliptic curve and its finite field for all users.

The parameters include the equation itself, a prime modulus for the field, and a base point on the curve. The order of the base point, which is not chosen independently but determined by the other parameters, can be visualised as the number of times the point is added to itself until its slope becomes infinite (a vertical line). The base point is chosen so that the order is a large prime.

For the base point, prime modulus and order, Bitcoin uses very large numbers. The scheme’s security relies on these values being huge, which makes brute force or engineering analysis impractical.

In Bitcoin:

Elliptic-curve equation: y2 = x3 + 7

Prime modulus = 2^256 – 2^32 – 2^9 – 2^8 – 2^7 – 2^6 – 2^4 – 1 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F

Base point = 04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8

Order = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141

This implementation is known as secp256k1, part of a family of elliptic curves over finite fields proposed for cryptographic use.

As Bitcoin’s current signature method, ECDSA lacks native support for multisignatures. They are implemented via the standardised smart contract Pay-to-Script-Hash (P2SH), which commits only script hashes to the blockchain.

This seemingly random number determines coin ownership. When spending, the holder reveals the script and the key to decode the hash at the same time. Anyone can then use the original hash to verify the script and enforce the spending conditions. However, users must disclose all spending conditions, including those not exercised. For example, coins may be spent if and only if Bob and Alice sign the transaction, or Alice signs it alone after a week, or Bob signs it by also providing a secret number.

The first problem is privacy. P2SH transactions require addresses that start with 3. This allows blockchain analysts to identify all P2SH transactions on the network and the addresses involved in multisignature spending.

The second problem is data heft, since P2SH requires the public keys of all multisignature participants to be known.

The Schnorr signature scheme and Taproot address these issues.