What is impermanent loss (IL)?

What is impermanent loss?

Impermanent loss (IL) is the temporary, notional loss that arises when providing liquidity to an automated market maker (AMM) on a decentralised exchange. It is the difference in the value of assets if simply held in a wallet (HODL) versus kept in a liquidity pool.

Impermanent loss appears mainly in classic pools where a liquidity provider (LP) must supply both assets in equal proportions and one asset is volatile relative to the other.

Impermanent loss using the DAI/ETH pool on Uniswap, where both tokens are supplied 50:50:

1. Deposit 1 ETH and 1,000 DAI into the pool.
2. A week later, 1 ETH equals 2,000 DAI.
3. Had we held 1 ETH and 1,000 DAI in a wallet, the return would be 50% (the 1,000 DAI would be unchanged, while 1 ETH would be worth 2,000 DAI).
4. Providing liquidity to an AMM pool on Uniswap yields less than the 50% return from simply holding the assets.

The losses are called impermanent or unrealised because they are not locked in until the liquidity tokens are withdrawn from the pool. In the example above, if ETH returns to the original 1,000 DAI and funds are then withdrawn, there is no impermanent loss.

Uniswap, SushiSwap and similar AMMs follow a simple formula:

x ∗ y = k

• x — the number of tokens of asset A;
• y — the number of tokens of asset B;
• k — the pool’s constant product; this value does not change.

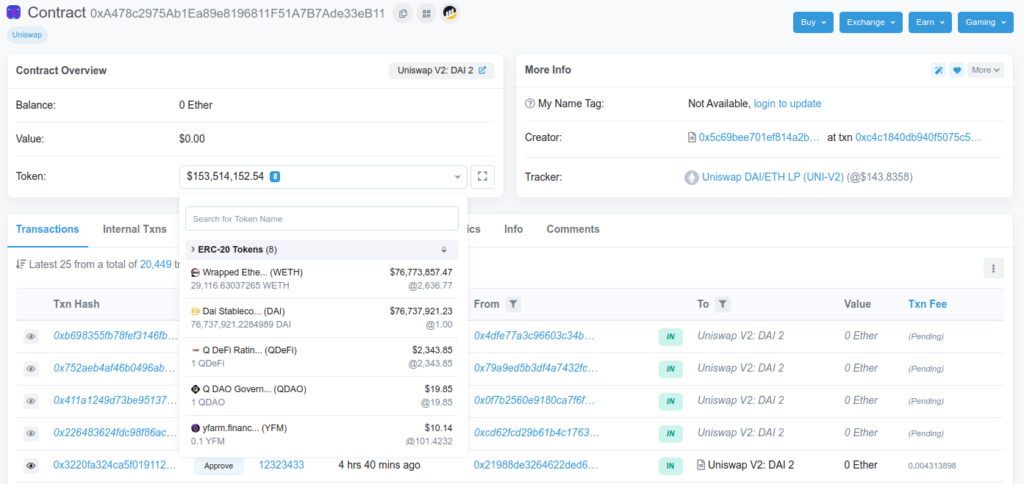
The contract held tokens worth about $153.5m — 29 116,6 WETH and 76,7m DAI.

Using the formula above, we compute k for this pool at that moment:

29 116,63 ∗ 76 737 921,22 ≈ 2,23 ∗ 10^12

k changes only when users add or withdraw liquidity, or when trading fees are charged (for example, 0.3% on Uniswap). Those fees accrue to the pool’s liquidity.

A detailed example of interacting with an AMM pool:

1. Deposit 1 ETH and 100 DAI into a Uniswap pool.
2. After that, total pool liquidity is 10 ETH and 1,000 DAI (the LP’s share is 10%).
3. Over a week, trades totalling 100 ETH occur in the pool (50% in ETH and 50% in DAI), but the ETH/DAI price does not change.
4. No liquidity is added to or removed from the pool during the week.
5. Total liquidity is now 10,15 ETH and 1,015 DAI, accounting for 0,3 ETH of accrued fees.
6. The LP’s share remains 10%, but the position has grown thanks to fee income.
7. If funds are withdrawn after a week, there is no impermanent loss because the ETH/DAI price ratio is unchanged.

Impermanent loss in classic pools

Example of Uniswap’s DAI/ETH pool:

1. Deposit 1 ETH and 100 DAI; the LP share is 10%.
2. The pool holds 10 ETH and 1,000 DAI.
3. A week later, 1 ETH trades at 200 DAI.
4. No trading fees in the pool.
5. Calculate impermanent loss.

First, compute k:

k = 10 ∗ 1000 = 10 000

Against DAI, ETH’s global price doubled. Arbitrageurs bought ETH cheaply from the pool. With demand rising and supply limited, the price of 1 ETH reached 200 DAI.

At the start of the week, when 1 ETH was 100 DAI, the pool held 10 ETH and 1,000 DAI. Let us find the new distribution after the price change. Set a few variables, starting with the price ratio between assets.

r_t = price of a in b,

where a and b are the two assets in the pool.

In our example, a is ETH and b is DAI. Initially, 1 ETH traded for 100 DAI, so the initial r is 100. Use t to denote the time at which r is measured.

Combining the equation above with the AMM’s constant‑product formula gives expressions for the quantities of each asset in the pool at any price ratio r at time t:

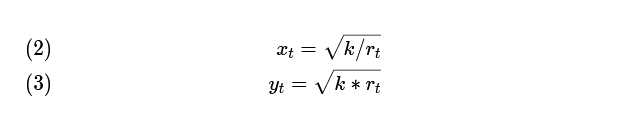
Apply these to the initial position:

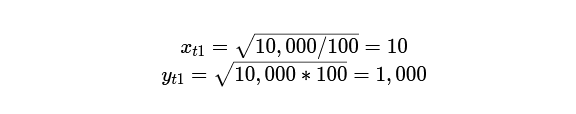
We recover the initial state — 10 ETH and 1,000 DAI. Now apply the same formulae at the end, when 1 ETH trades at 200 DAI. The new r is 200. Substitute it:

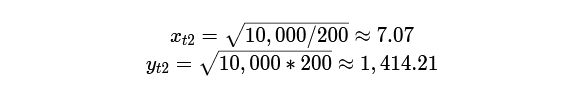
After the price change, the pool holds about 7 ETH and about 1,414 DAI. A quick check:

7,07 * 1414,21 ≈ 10 000

The constant‑product equation still holds. Our share is 10%, so after the change we are entitled to 0,707 ETH and 141,421 DAI.

If the assets (1 ETH and 100 DAI) were simply held, their value would be $300. The dollar value of the pool position is:

0,707 * 200 + 141,421 = 282,821

Using this, the impermanent loss is:

300 — 282,821 = 17,179

17,179/300 ≈ 0,0572 ≈ 5,72%

17,179 DAI, or about 5.72%, is what we would have earned by simply holding rather than providing liquidity. There is a gain on the initial 200 DAI position, but holding would have been more profitable.

A simple formula to compute impermanent loss:

staking_USD/holding_USD — 1

Apply it to our example:

282,821/300 -1 ≈ -0,0572 ≈ -5,72%

To find the exact pool share (in each token), use formulae (2) and (3), the analytics platforms Uniswap Analytics and SushiSwap Analytics, or third‑party tools Croco Finance, Growing and APY.vision.

Why pool fees matter

The previous example ignored trading fees. That simplifies the maths, but fees should be accounted for; they are integral to AMM economics.

The higher the fee income, the smaller the impermanent loss. Beyond a certain level of fees, providing liquidity outperforms holding.

Take the example above and add fees:

1. Deposit 1 ETH and 100 DAI in the pool;
2. Our share is 10% (the pool has 10 ETH and 1,000 DAI);
3. A week later, 1 ETH trades at 200 DAI;
4. Fees accrued: 1 ETH and 100 DAI.

Without fees, the impermanent loss is 17,179 DAI. With a 10% share, we are entitled to 0,1 ETH and 10 DAI from fees. At 200 DAI per ETH, 0,1 ETH is 20 DAI, so total fee income is 30 DAI. The total is therefore $312,821 ($282,821 + $30).

Plug these numbers into formula (4):

312,821/300 — 1 ≈ 0,042 ≈ 4,2%

In this example, the impermanent loss is −12,821 DAI (17,179 — 30). Thanks to fees, providing liquidity yields a 4.2% gain versus holding.

What formula is needed to plot impermanent loss?

So far we have used the simple formula (4) to compute IL. It is fine for the current IL, but awkward when you want IL at different prices.

From formulae (1), (2) and (3) you can derive another expression that makes IL calculations easier:

Apply it to our example. We know the initial r is 100 (1 ETH trades for 100 DAI) and the final r is 200. Hence p equals 0.5 (100/200). Use these values:

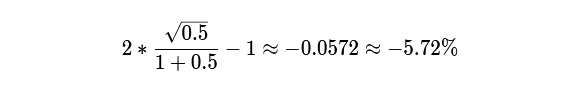
This matches the number from formula (4). Varying p yields IL for different price moves.

This formula does not include trading fees. To plot IL with fees, use:

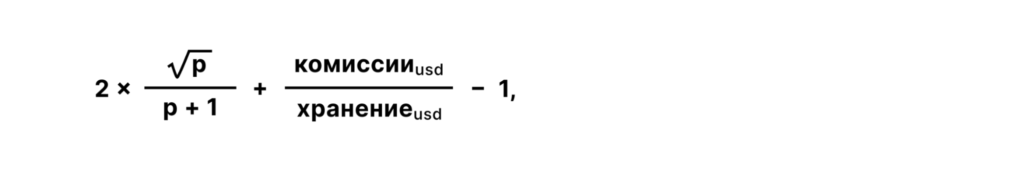
Fees can be estimated from APY data provided by some AMM platforms.

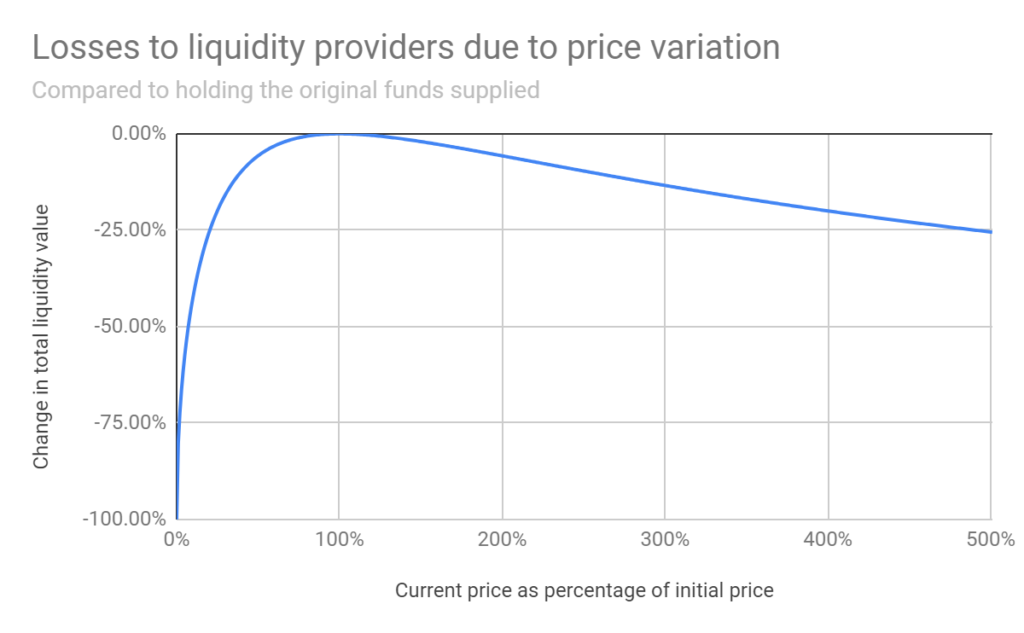
The chart below illustrates IL for various price changes. For example, a fivefold move implies 25.5% IL; a twofold move, 5.7%.

Does impermanent loss work the same way in other pools?

Curve is a decentralised exchange for stablecoins and tokenised bitcoin built on an AMM. Its pools contain only assets that should have the same or comparable value: stablecoins (USDC, DAI) or tokenised bitcoin (renBTC, wBTC). The risk of impermanent loss in such pools is minimal.

Balancer offers pools with arbitrary weightings of tokens. If a liquidity provider wants to supply large amounts of a particular token, they can choose a pool where that coin has a higher weight than others (for example, 80/20 or even 98/2). This also minimises impermanent loss. The larger a token’s weight in the pool, the smaller the gap between holding the token and providing liquidity in it.

Bancor’s second‑generation pools automatically adjust token weights based on oracle data. This helps minimise impermanent loss even in pools with volatile assets.

How to estimate impermanent loss easily

Anyone using AMM platforms should understand impermanent loss. You can run your own IL calculations with a calculator at dailydefi.org (based on Uniswap’s formulae).

In general, AMM users are always exposed to the risk of opportunity cost, regardless of price direction. Compared with holding, when prices rise an LP’s position appreciates more slowly; when prices fall, losses are larger.

Trading fees and yield farming help offset impermanent loss so that participating in an AMM pool can outperform simply holding assets.